So I am one to sometimes meddle with making roleplaying systems (in fact I’ve been playing games in that system for years now) but in the afterglow of storytelling at PrinceCon for the first time in a long time, I more seriously started to ponder about dice. The PrinceCon system — now with more than 40 years of history behind it — presently runs off of a d20 OGL-based system which (like all d20-based games) resolves randomness with a roll of a 20-sided die, plus modifiers, to meet or exceed a difficulty.
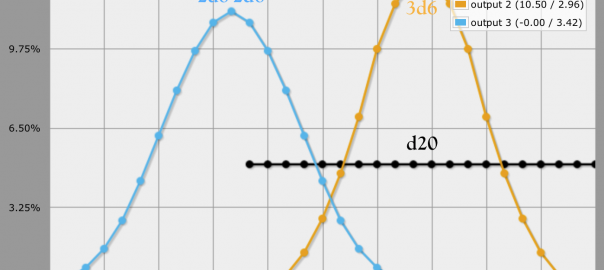
A single die roll, of course, is a completely flat distribution. You have a 5% chance to land on any one number and a 50% chance to roll an 11 or higher.
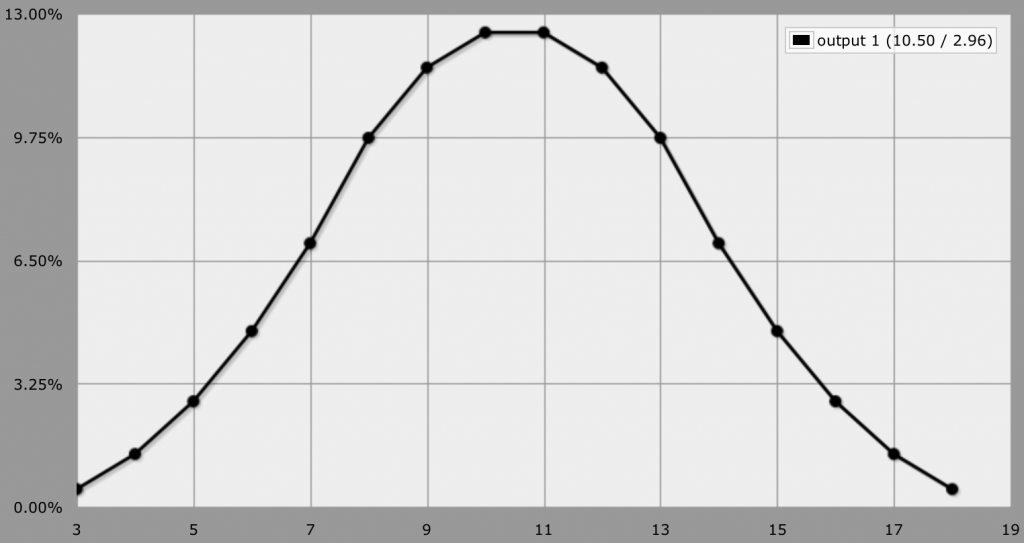
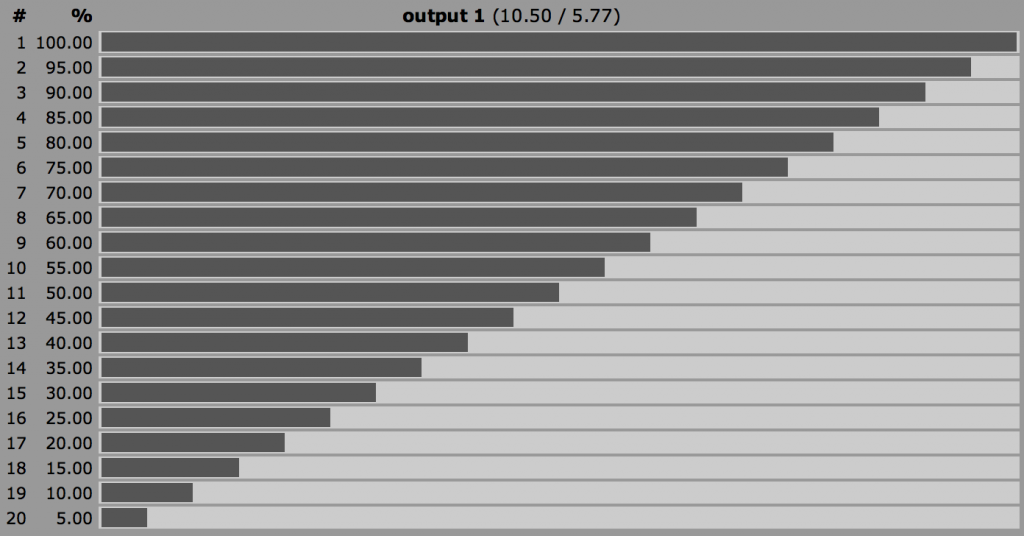
The 3d6 bell curve. From anydice.com.
I’m not one who likes flat distributions (they’re all over the place) so when I play d20 I tend to play with the 3d6 variant, which makes a nice bell curve (seen above) whose peak falls betwixt 10 and 11, and whose extremes (3 and 18) have a mere ~0.5% chance of happening.

Probabilities for landing at least on the number listed for 3d6. From anydice.com.
This works well for many things, but it’s not as elegant as a d20 in some respects. First, a d20 has a range of 20 values. In a system where a value of 10 is average (like d20 OGL) that works out well. 3d6 only has a range of 16 values (3-18), so it is much shorter and by default, difficulties below 3 are impossible (which effectively takes out a chunk of range). Furthermore, none of the values on the curve are nice “round numbers.” Getting a 10 (base) is a 62.5% chance, getting a 15 (+5 base) is ~5%, and getting an 18 (+8 base) is about 1 in 200.
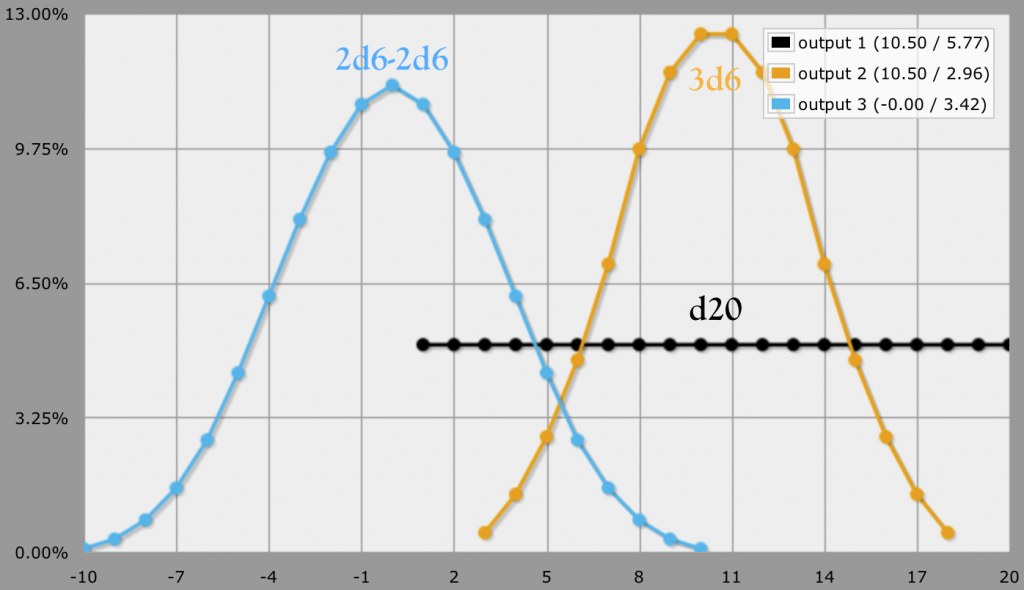
Playing around with probabilities on AnyDice.com (awesome site) I fiddled around with different possible dice combinations and unexpectedly found that 2d6-2d6 might present a more elegant solution.
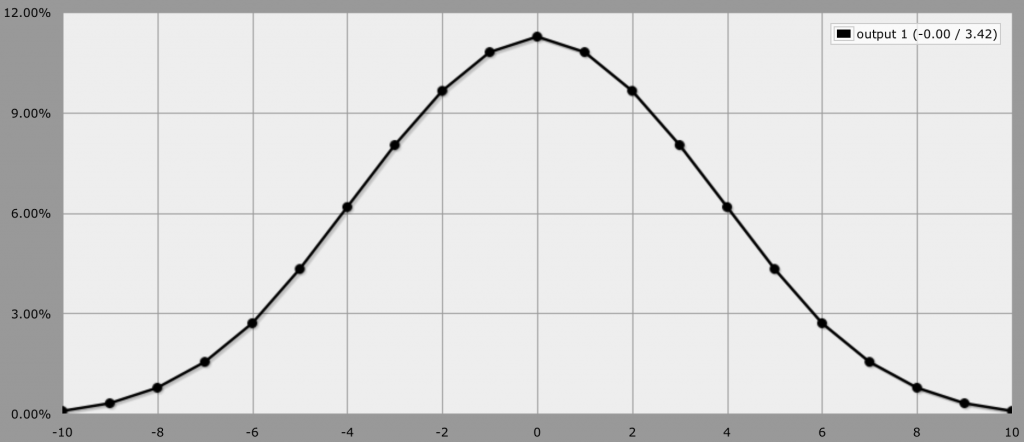
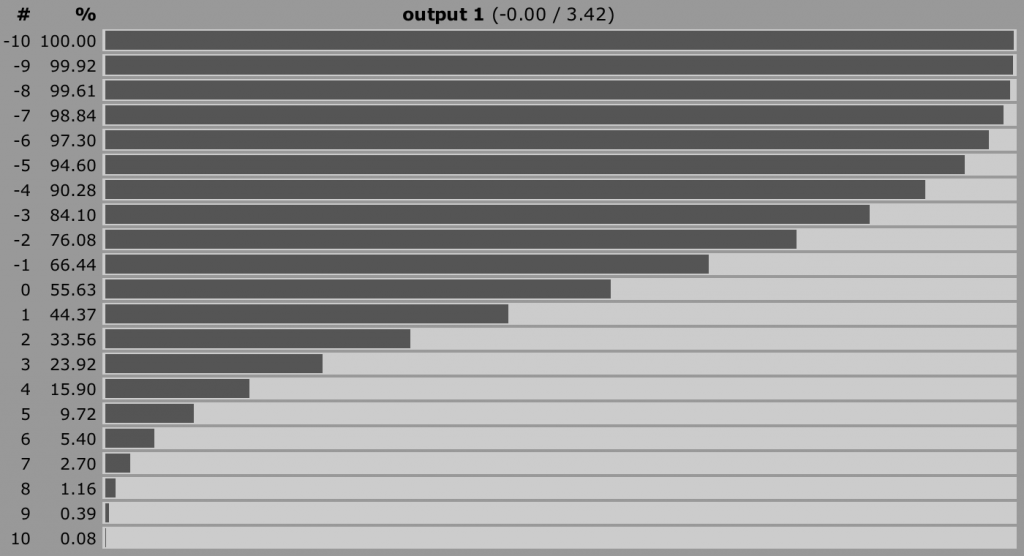
2d6-2d6 bell curve. From anydice.com.
Where it seems like a lot of dice (and a bit more math) 2d6-2d6 creates a beautiful graph with some elegant properties.
- First of all, it’s a nice bell curve.
- Second, the peak of the bell curve is on 0, so all results will fall around the base modifier. In a system where the base statistic is 10 that means that a roll will range between 0 and 20 (just like d20, albeit 0 is possible).
- Third the major increments fall upon rather round probabilities:
- About 90% of the time you’ll at least hit -4 or more.
- About 75% of the time you’ll hit -2 or more.
- About 2/3rds of the time you’ll hit -1 or more.
- Base probability (0) is 55% (as close to half as one can get)
- +2 is almost exactly 1 in 3
- +3 is roughly 25%
- +5 is roughly 10%
- +6 is roughly 5%
- +7 is roughly half that (~2.5%)
- +8 is roughly 1%
- +9 is roughly 1 in 250; and for something truly epic
- +10 is roughly 1 in 1000
This progression makes incremental changes to the difficulty of a task ease into a curve with some nice round numbers. 🙂
And given that the extremes happen so rarely, it gives a good excuse for an epic resolution as they really are a one-in-a-thousand shot.
Now, this has direct application to d20-like games. The only thing that would have to change is the calculation of base skill levels and roll modifiers as now everything would need to start out at a base of 10. In the end you would get the same range as a d20, but with a nice bell curve.
| Mean | Deviation: | Range: | |
|---|---|---|---|
| d20 | 10.5 | 5.7 | 20 [1-20] |
| 3d6 | 10.5 | 2.96 | 16 [3-18] |
| 2d6-2d6 | 0 | 3.42 | 21 [-10-10] |
As such I believe that there is some good potential for using 2d6-2d6 as a base roll for table-top RPGs.
Peace,
-Steve